树的概念

树（Tree）是n个节点的有限集合，n=0为空树，在非空树中，有以下特征：

  1. 有且仅有一个称为根（root）的结点；
  2. 除了根结点之外，其余结点可分为多个（m个）互不相交的有限集合，每个集合也是一个树，称之为根的子树（SubTree）。
树的展示

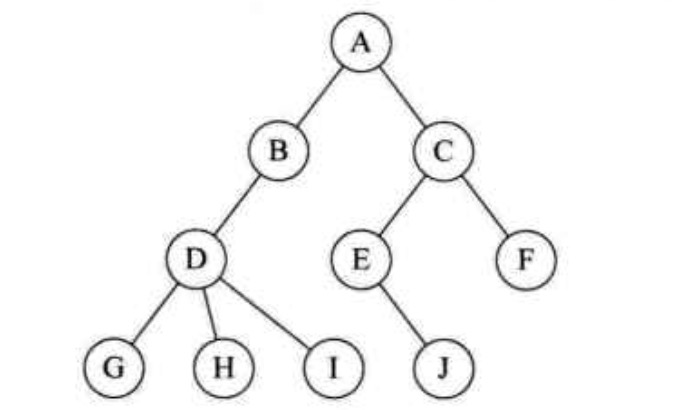
可以用递归的思想来理解树，一个树下面又是其他树，每个树下都套这多个树。

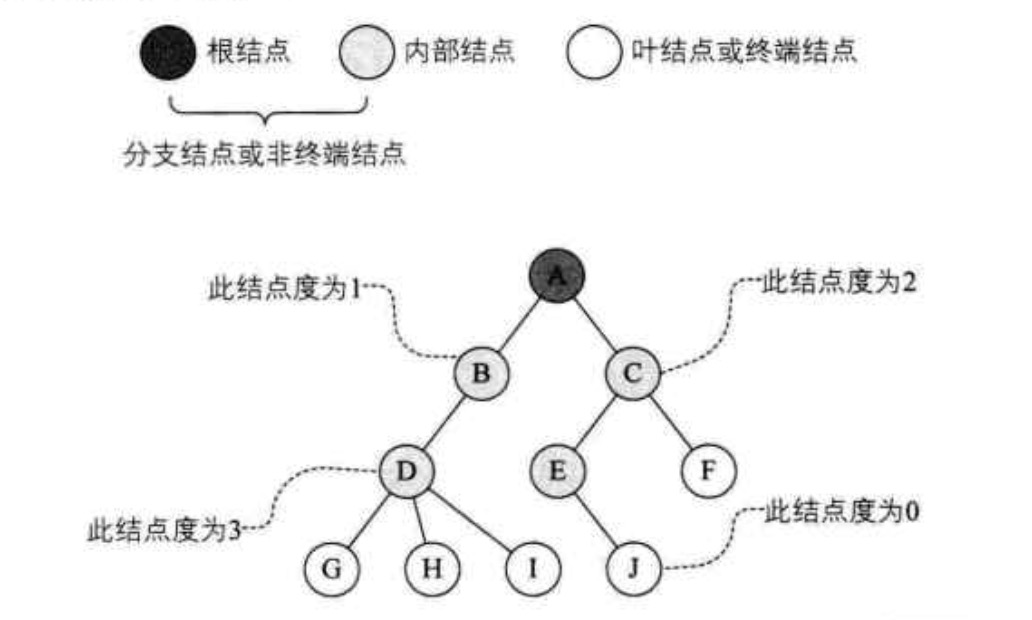
树的几个概念说明：

  • 结点的度： 结点拥有的子树数目
  • 叶结点： 度为0的结点称为叶结点或终端结点
  • 分支结点： 度不为0的结点为分支结点或非终端结点
  • 树的度： 树内各结点的度的最大值
  • 结点的孩子（Child）： 结点的子树的根称为该结点的孩子，而该结点称之为孩子的双亲（parent）
  • 兄弟结点： 同一双亲的孩子称为兄弟（Sibling）
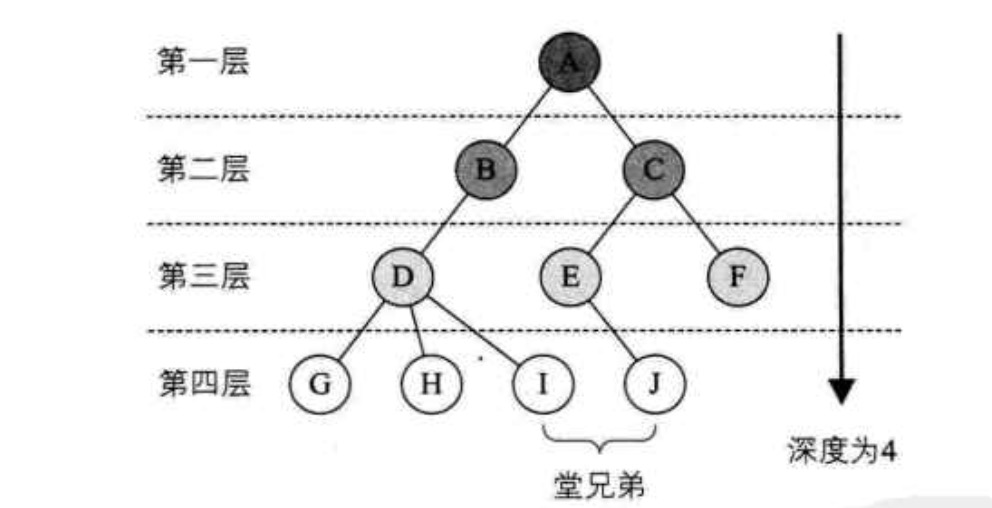
  • 结点的层次： 从根开始定义，根为第一层，根的孩子为第二层，以此类推
  • 树的深度： 树中结点的最大层次称为树的深度（Depth）或高度

参考下图：

二叉树的定义

二叉树（Binary Tree）是n个结点的有限集合，n=0为空树，在非空树中，由根结点和两颗互不相交的，分别称为根结点的左，右子树的二叉树组成。

通俗的来说二叉树，即一颗树的每个结点的度最大为2，即树的度最大为2。

二叉树的特点

  • 每个结点最多两颗子树。
  • 左子树和右子树是有顺序的，次序不能任意颠倒。
  • 即使树中某结点只有一颗子树，也要区分是左子树还是右子树。

二叉树的实现

二叉树使用顺序存储的适用性不强，这里用链式的存储结构。

二叉树结点的定义

二叉树最多右两个孩子，因此定义一个数据域和两个指针域：

1
2
3
4
5
class BiNode:
    def __init__(self, data):
        self.data = data
        self.lchild = None
        self.rchild = None

BiNode中，data是数据域，lchild和rchild为指针域，分别存放指向左，右孩子的地址指针。

二叉树的遍历

二叉树的遍历一般分为，前序遍历；中序遍历；后序遍历
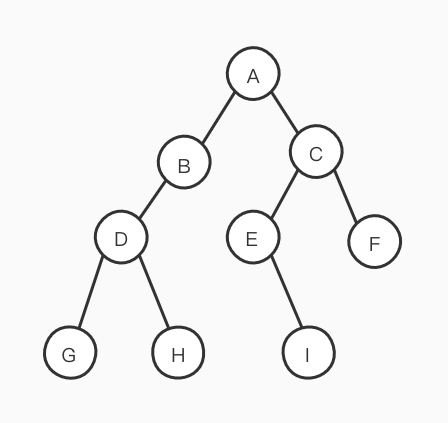
下面描述以下这些遍历，假设一个非空二叉树：

一个二叉树

  • 前序遍历
    先访问根结点，然后遍历左子树，最后遍历右子树。上图中，遍历顺序为：ABDGHCEIF

  • 中序遍历
    从根结点开始（但并不是先访问根结点），先遍历左子树，然后访问根结点，最后遍历右子树。上图中，遍历顺序为：GDHBAEICF

  • 后序遍历
    先从左到右遍历左右子树，最后访问根结点。上图中，遍历顺序为：GHDBIEFCA

通过图片可以很直观的看到遍历的过程。而在计算机程序中，要实现这样的遍历，最方便的就是使用递归来遍历。

二叉树遍历的代码实现

  • 前序遍历
    1
    2
    3
    4
    5
    6
    7
    8
    def pre_travel(root):
        """前序遍历"""
        if root == None:
            return

        print(root.data) # 先展示结点数据
        pre_travel(root.lchild) # 遍历左子树
        pre_travel(root.rchild) # 遍历右子树
    代码非常简单，先读取一个树的根结点，然后遍历这个结点的左子树，继续遍历这个结点的右子树，接下来继续递归这样的操作。
    以上图为例，来看下程序是如何运行的。
  1. 一开始进入函数，传入根结点A，发现不是空，先打印该结点的数据：A
  2. 下面遍历根结点的左子树即结点B，B不为空，打印该结点的数据：B
  3. 遍历结点B的左子树即结点D，D不为空，打印该结点的数据：D
  4. 遍历结点D的左子树即结点G，G不为空，打印该结点的数据：G
  5. 遍历结点G的左子树，发现为空，返回，结点G的左子树遍历结束；开始遍历结点G的右子树，也为空，返回，结点G的右子树遍历结束。
  6. 结点D的右子树即结点H，H不为空，打印该结点的数据：H
  7. 遍历结点H的左子树，发现为空，返回，结点H的左子树遍历结束；开始遍历结点H的右子树，也为空，返回，结点H的右子树遍历结束。
  8. 结点D的左右子树遍历结束，返回；下面遍历结点B的右子树，发现为空，返回，结点B的右子树遍历结束。
  9. 结点B的左右子树遍历结束，返回；下面遍历根结点A的右子树，即结点C，C不为空，打印该结点的数据：C
  10. 和遍历根结点A的左子树一样遍历右子树，可以得到结果EIF

  • 中序遍历

    1
    2
    3
    4
    5
    6
    7
    8
    def pre_travel(root):
        """前序遍历"""
        if root == None:
            return

        pre_travel(root.lchild) # 遍历左子树
        print(root.data) # 先展示结点数据
        pre_travel(root.rchild) # 遍历右子树

    可以看到，这次是先遍历左子树，然后打印结点数据，最后遍历右子树

  • 后序遍历

    1
    2
    3
    4
    5
    6
    7
    8
    def pre_travel(root):
        """前序遍历"""
        if root == None:
            return

        pre_travel(root.lchild) # 遍历左子树
        pre_travel(root.rchild) # 遍历右子树
        print(root.data) # 先展示结点数据

二叉树的建立

为了让每个结点确认是否有左右孩子，需要对二叉树进行扩展。需要标识空结点，这里用#来表示空结点的数据值。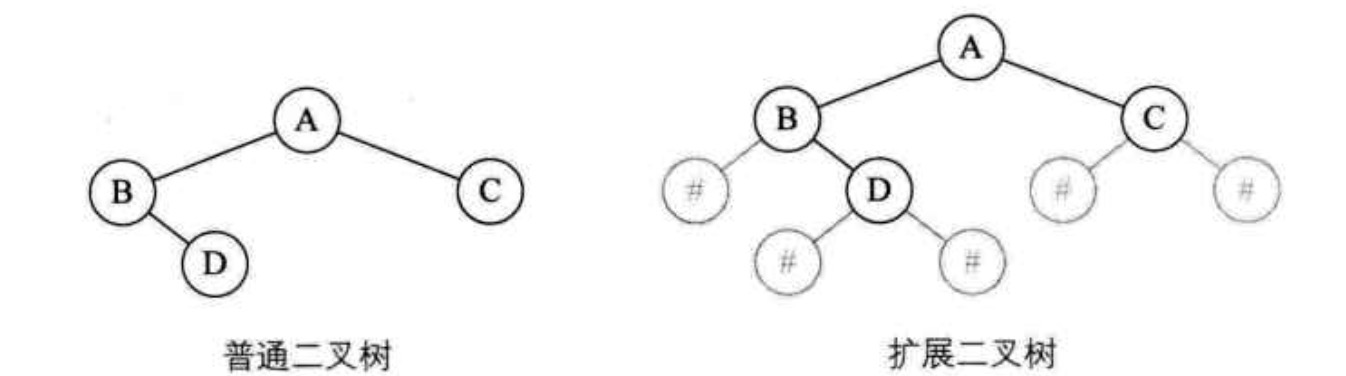

普通二叉树的前序遍历结果为：ABDC
扩展二叉树的前序遍历结果为：AB#D##C##

根据扩展二叉树的前序遍历来创建二叉树

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
class BiTree:
    def __init__(self, root=None):
        self.root = root

    def create_tree(self, definition):
        self.root = None
        self._definition = definition
        self._definition_index = 0
        self._pre_create_tree()

    def _pre_create_tree(self):
        """前序插入创建"""
        if self._definition_index >= len(self._definition):
            return None

        char = self._definition[self._definition_index]

        if char == '#':
            return None

        node = BiNode(char)
        if self.root is None:
            self.root = node
        
        self._definition_index += 1
        node.lchild = self._pre_create_tree()
        self._definition_index += 1
        node.rchild = self._pre_create_tree()

        return node

使用中序遍历得到：BDAC
使用后序遍历得到：DBCA

二叉树介绍到此为止，python的实现代码可参考：
https://github.com/dougaoyang/struct_code/blob/master/btree.py